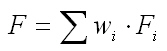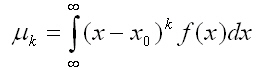
It handles an approximation of the output function to the Taylor-series about its mean values. This is analytical methods calculating the distribution of output from the distributions of inputs. The center moments of outputs are derivate from the k-order center moments of inputs µ.
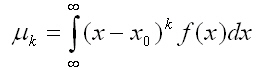
From these calculated moments, the output distribution density function can be fitted using well known table. Because the methods work without random numbers and therefore it is very stable. It allows a fast and stable probabilistic optimization with stochastic variables. The methods deliver quite accurate results, if the correlation between inputs and outputs in the tolerance space is approximately linear or quadratic. The results of this tolerance analysis methods for 4 tolerances can compare with results of Monte-Carlo-sampling with 100 000 samples size. There are 2 classes of these methods implemented in OptiY:
The output function is approximated to the Taylor series of first order. If f is the function with n variables x, then the first order Taylor series can be written down:
This method is called second order tolerance analysis, which bases on the approximated second order Taylor series of the problem. If f is the function with n variables x, then the second order Taylor series can be written down:
Interaction
If the interaction between inputs exist, the linear interaction between pair wise inputs for the both method classes can be considered. The output function f is added with the crossing derivatives:
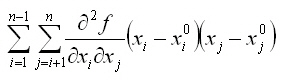
Model Calculations
|
Methods |
Correlation | Model Calculations without Interaction | Model Calculations with Interaction |
| First Order | linear | n+1 | 2n2-n+1 |
| Second Order | quadratic | 2n+1 | 2n2+1 |
System Failure Probability
The partial failure probability of single constraints Fi can be here calculated accurate, because the constraint distribution density function is known. But, the system failure probability of all outputs F derivate by these methods cannot be calculated accurately. Therefore, the surrogate failure probability using only for optimization is implemented with the weighting factors wi of single constraints: