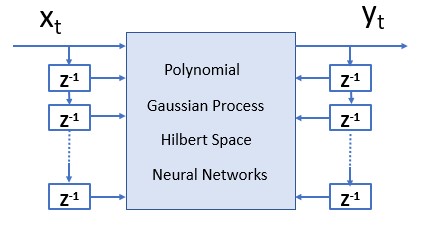
The nonlinear autoregressive exogenous (NARX) model is a type of time-series modeling that combines autoregressive components with exogenous variables [113-115]. In a traditional autoregressive (AR) model, the value of an output variable at a given time is predicted based on its past values. The order of the AR model determines how many past output values are considered. The NARX model extends the concept of autoregressive modeling by incorporating exogenous input variables, which are external factors that can influence the output variable being predicted. These exogenous variables can be additional time-series data or any other relevant features that are believed to impact the target variable. By including exogenous variables, the NARX model can capture nonlinear relationships and improve the accuracy of predictions.
The general model function can be defined as:
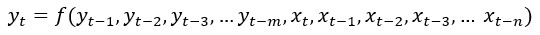
Where m is the output order, and the n is the input order.
The NARX model can be trained using various techniques, such as neural networks or nonlinear regression algorithms. The specific structure and architecture of the NARX model can vary depending on the implementation and the problem at hand. This specific model presents a data-driven discovery of partial differential equations for physics given by collected data. Overall, the NARX model is a flexible and powerful approach for time-series modeling, particularly when the relationships between variables are nonlinear and influenced by external factors.