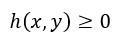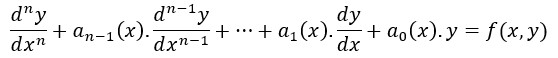
Physics-informed machine learning (PIML) is an approach that combines principles from physics and machine learning to leverage the benefits of both fields. It is used to incorporate physical laws, boundary, initial conditions, constraints, and prior knowledge into machine learning models, allowing for more accurate predictions and improved generalization [92-112]. Traditional machine learning techniques rely solely on data-driven patterns to make predictions [27]. However, in many scientific and engineering applications, there is valuable domain-specific knowledge about the underlying physical processes governing the data. Physics-informed machine learning aims to exploit this knowledge to enhance the learning process. In PIML, physical laws and constraints are incorporated into the machine learning framework in the form of additional terms in the loss function or as regularization terms. These terms help guide the learning process and ensure that the resulting models are consistent with the known physics. By incorporating physical constraints, PIML can make predictions that are not only accurate but also physically meaningful.
The benefits of physics-informed machine learning include improved interpretability, better generalization to unseen scenarios, and the ability to make predictions in data-scarce regimes where traditional machine learning approaches may struggle. By combining the power of machine learning with the foundational understanding provided by physics, PIML has the potential to revolutionize various scientific and engineering disciplines.
Partial differential equation (PDE) is the mathematical equation that describes the behavior of physical systems and phenomena, often involving multiple variables and their derivatives with respect to space and time. They are fundamental in expressing the laws of physics governing various natural phenomena, such as fluid dynamics, electromagnetism, heat transfer, and quantum mechanics. PDE provides a mathematical framework to describe the relationships between the 0various physical quantities involved in a system and how they change with respect to space and time. These equations encapsulate the fundamental principles, conservation laws, and underlying physics of the systems they represent.
Solving PDE analytically is often challenging and limited to simple cases. However, numerical methods have been developed to solve PDE computationally. Finite difference, finite element, and finite volume methods are some common techniques used to approximate solutions to PDE on a discretized grid. Physics-informed machine learning (PIML) builds upon this foundation by incorporating PDE into the machine learning framework. By using PIML, the underlying physics encoded in the PDE can be leveraged to enhance the learning process and improve the accuracy and generalization of machine learning models. This PIML represents a data-drive solution of partial differential equation.
The general nonlinear partial differential equation of order n for input vector x and output variable y can be defined as:
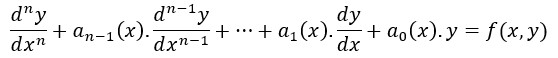
subject to general boundary or initial conditions
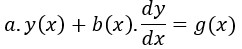
and constraints