Several stochastic probability distributions have been implemented in OptiY to describe the property representing a variability and uncertainty of the design parameters. Normal and uniform distributions are frequently used. Using the generalized lambda distribution, a arbitrary distribution can be modeled for stochastic variables by setting of its parameters.
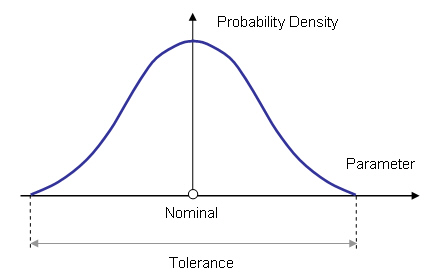
Normal Distribution
This is a Gaussian distribution. The normal distribution will occur frequently by mass manufacturing process, if the number of pieces is high enough. The tolerance is defined as six standard deviations sigma: T = 6 · σ. The nominal value of design parameter lies in the center of distribution.

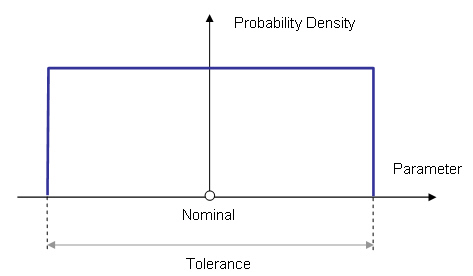
Uniform Distribution
Another frequently used stochastic variable is the uniform
distribution. The nominal value of design parameter
lies in center of distribution. The context between tolerance value and
standard deviation is:
![]()
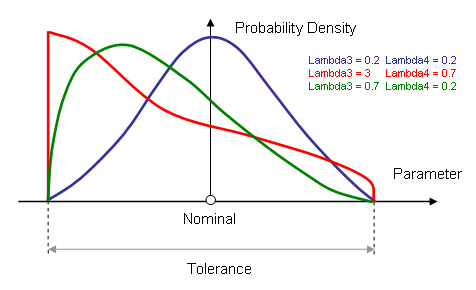
Generalized Lambda Distribution
This is a generic lambda distribution [16]. The quantile function and probability density function are described below:
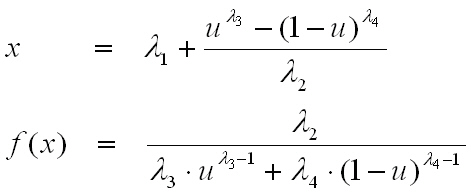
u is a uniform random variable 0<u<1. A arbitrary distribution form can be modeled by setting the lambda parameters Lambda1, Lambda2, Lambda3 und Lambda4. Lambda1 is the location and Lambda2 is the scaling factor of the distribution. Lambda3 und Lambda4 represent the form of the distribution. A symmetric distribution results from Lambda3=Lambda4. Interchanging the positions of Lambda3 and Lambda4, the distribution form will reflect on the location Lambda1. The tolerance value is intern fixed at: T = 2/Lambda2 and the mean value is always the nominal value. There are some orientation values of lambda parameters below: