Sampling Methods
It deals with stochastic simulation via random number
generator. There are three types of sampling methods:
Tolerances can be modeled by stochastic variables
generated by a random number generator according a
tolerance distribution. Inside of
a tolerance range, a set of random numbers are generated as a samples size for
the inputs. For each sample, a simulation run must be executed to determine the outputs.
After
running all samples, distributions of the outputs can be evaluated.
With the Monte Carlo sampling, a intensive derivation of
partial derivatives of a complex tolerance chain can be avoided for a arbitrary
problem. The accuracy of the method depends on the samples size, which should be
defined exponential to the number of tolerances. This method is used very
universal, but associated with a intensive computational effort. For simulation
models, which runs over hours, the method is hewer unsuitable.
This method is also a Monte Carlo sampling. The difference
results from the generating of random numbers for inputs. At Monte Carlo
sampling, the whole range of tolerances is used generating random numbers. At
Latin Hypercube sampling however, the accumulated distribution function is
divided in N equal intervals. For each interval, a random number is generated.
With this method, a small samples size (e.g. 50) can generate a good
distribution form. The below pictures show a normal distribution being generated by
Monte Carlo and Latin Hypercube sampling with 50 samples size.
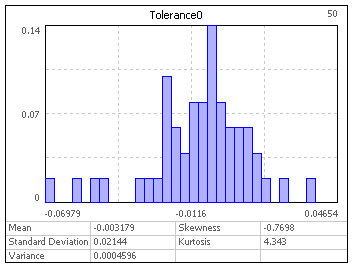
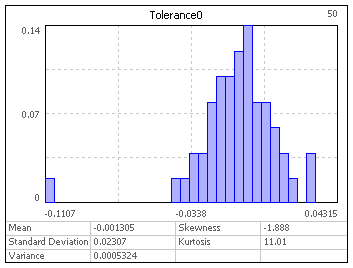
Monte Carlo Latin Hypercube
Sobol sampling is also Monte Carlo simulation. The
difference results from distribution of the random numbers in the parameter space.
The
method uses a quasi random number generator. Therefore, the generated numbers
scatter more uniformly in the parameter space then the Monte Carlo sampling (pictures
below). Sobol sampling needs smaller samples size (approximately 10%) for the
same accuracy like Monte Carlo sampling. The method can used by problems with
2-40 tolerances.
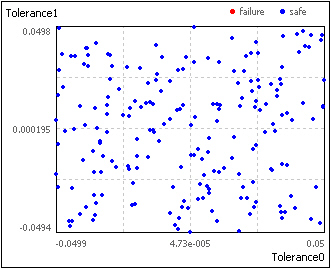
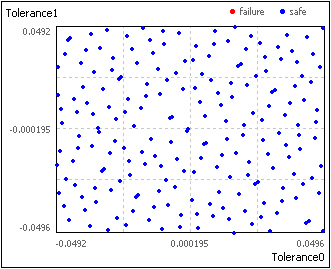
Monte Carlo Sobol



